Capacity planning não é sobre prever o futuro com precisão absoluta. É sobre entender os limites estruturais do sistema antes que eles se tornem incidentes. A maioria dos problemas de capacidade não surge de crescimento repentino, mas da incapacidade de interpretar o comportamento do sistema sob carga real. Métricas isoladas, como CPU, memória ou TPS médio, raramente contam a história completa. O que realmente importa é como esses sinais se relacionam, como a concorrência interna se acumula e onde os gargalos se formam quando a carga deixa de ser uniforme.

Passei os últimos 3 meses do ano de 2025 procurando modelos matemáticos para me guiar nos assuntos de capacity planning e performance para minha caixa de ferramentas. Aqui, guardo um compilado dos conceitos e fórmulas mais relevantes que encontrei. Rascunhei este capítulo logo em seguida a uma das etapas mais intensas do meu mestrado, e seu resultado final foi uma linguagem muito mais densa e teórica do que os anteriores, mas gostei muito do resultado.

Este texto não é um guia para dimensionar servidores. É uma abordagem sistemática para modelar carga, interpretar saturação e planejar crescimento de forma estruturada. A teoria das filas, a Lei de Little e a curva do joelho não são apenas abstrações acadêmicas, são ferramentas práticas para responder perguntas como “quanto meu sistema aguenta de forma sustentável?” e “onde ele quebra antes de eu perceber?”. O objetivo é transformar capacity planning de uma reação a incidentes em uma prática de engenharia preventiva e bem fundamentada.

Teoria das Filas

A teoria das filas é um dos fundamentos mais importantes e mal compreendidos em capacity planning. Em termos simples, a teoria estuda como sistemas se comportam quando múltiplas demandas competem por recursos finitos. Em engenharia de software, podemos utilizar como base comportamentos comuns, como requisições síncronas aguardando processamento para responder a um cliente, mensagens acumuladas em filas, múltiplos itens sendo processados em memória, conexões disputando pools limitados em bancos de dados ou operações de I/O esperando acesso a um recurso compartilhado.

De forma conceitual, toda fila pode ser entendida a partir de três dimensões: como as demandas chegam ao sistema, como elas são processadas e em que ordem são atendidas. O objetivo é transformar arquiteturas complexas em modelos matematicamente analisáveis, principalmente em arquiteturas distribuídas, onde taxas de uso estáveis e tempos de resposta previsíveis raramente se sustentam de forma consistente.

As “filas” não existem apenas onde há estruturas literais de enfileiramento assíncrono, como brokers de mensagens e eventos. Embora a teoria das filas seja vista apenas como uma abstração acadêmica na maior parte dos casos, ela nos fornece formas de compreender gargalos, throughput real, tempo de resposta e latências em cascata decorrentes de cenários como saturação de pools de threads, conexões de banco de dados, locks em recursos compartilhados e mecanismos de retry, não apenas de forma isolada, mas sobretudo em arquiteturas distribuídas, onde cada hop, cada requisição, cada buffer e cada microserviço se comporta como uma fila independente, com sua própria taxa de chegada, taxa de processamento, saturação e congestionamento.

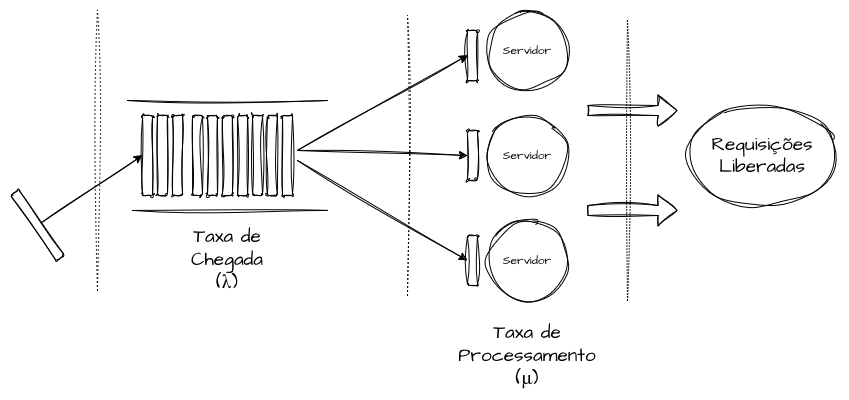
Da forma mais simples, uma fila é um mecanismo onde solicitações chegam (λ) e são processadas (μ), e o sistema oscila continuamente entre estados de ociosidade, equilíbrio e saturação dentro desses dois parâmetros. Quando a taxa de chegada (λ) se aproxima ou ultrapassa o limite da taxa de processamento (μ), isso gera um gargalo físico, onde tempos de resposta aumentam e o throughput degrada por haver uma taxa de envio maior do que a taxa de vazão. É por esse tipo de detalhe técnico que um microsserviço saudável em p95 pode degradar de forma significativa em p99 sob picos inesperados, mesmo com CPU e outros recursos aparentemente estáveis. No geral, o problema não é a falta de capacidade física, mas sim a variabilidade temporal, bursts e o custo de espera entre chamadas e processos.

Isso explica por que o autoscaling normalmente não resolve todos os problemas de capacidade, uma vez que ele reage apenas a aumentos expressivos de uso ou saturação de recursos para adicionar ou remover réplicas de um serviço. O autoscaling, de forma superficial, aumenta a taxa de processamento (μ) momentaneamente, permitindo que a taxa de vazão cresça, mas ainda funciona com base em gatilhos temporais, deixando o sistema sensível a bursts e picos de uso. Em outras palavras, um sistema não sofre porque recebe “muitas requisições”, mas porque recebe requisições de forma imprevisível ou não uniforme.

A teoria das filas propõe o uso de métricas de variabilidade, como o coeficiente de variação ou o desvio padrão, em vez de medidas como percentis, mínimos, máximos e médias na taxa de processamento. Analisamos, então, a variação da taxa de chegada (λ) e da taxa de processamento (μ). Essa visão explica por que sistemas com a mesma capacidade de recursos podem apresentar comportamentos completamente distintos sob carga real. Dois serviços com a mesma taxa média de atendimento podem exibir curvas de latência radicalmente diferentes se um deles processar requisições com desvio padrão elevado.

Estratégias já discutidas anteriormente, como sharding, bulkheads, caching, escalabilidade vertical e horizontal, desacoplamento por meio de filas e eventos, aumento do número de consumidores, bem como estratégias de concorrência e paralelismo, nos ajudam a lidar com a estabilidade dos sistemas quando a taxa de chegada supera a taxa de processamento.

A Lei de Little na Teoria das Filas

A Lei de Little, ou Little’s Law, é um princípio matemático simples integrado à Teoria das Filas, apresentado por John D. C. Little na década de 1960, que nos fornece insights valiosos para entender o comportamento de qualquer sistema sob carga. A lei não foi inicialmente formulada para conceitos computacionais complexos; ela pode ser utilizada para analisar a pressão de qualquer tipo de sistema sob a ótica da média de três variáveis, sendo elas o número médio de itens em processamento no sistema (L), a taxa média de chegada (λ) e o tempo médio de processamento e permanência desses itens (W) no sistema. Essa relação é expressa pela equação:

\begin{equation} L = \lambda \times W \end{equation}

Esse cálculo, por mais que seja simples, é válido para interpretar qualquer sistema estável, pois independe de estatísticas complexas e de valores exatos da taxa de processamento e permanência (W) e da taxa de chegada de itens ao sistema (λ), desde que suas médias sejam bem definidas.

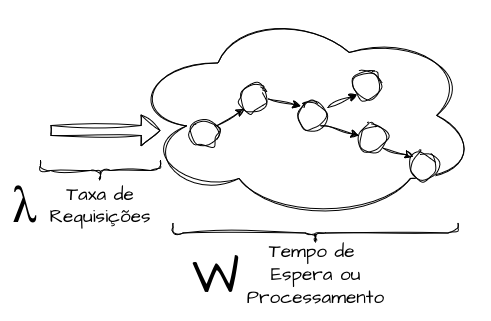
Em sistemas distribuídos, a Lei de Little nos ajuda a interpretar a capacidade de forma granular, a nível de cada componente, dependência ou microserviço, ou de forma mais ampla, analisando um fluxo completo em cenários onde estimar as capacidades exatas de todos os componentes pode ser muito complexo ou inviável.

Em termos práticos, ela se resume a uma interpretação adicional de capacidade sobre throughput e latência. Para uma taxa de chegada fixa (λ), qualquer aumento no tempo médio de resposta (W) implica, de forma imediata, um aumento proporcional no número de processos simultâneos (L) no sistema.

Considere um sistema assíncrono que recebe uma taxa média de 1.500 mensagens por segundo, com tempo médio de processamento por mensagem de 50ms. Aplicando a Little’s Law, podemos encontrar o número de processos concorrentes dentro do mesmo segundo:

\begin{equation} L = 1.500 \times 0.05 \end{equation} \begin{equation} L = 75 \end{equation}

Neste cenário, o sistema mantém, em média, 75 mensagens simultaneamente em processamento ou espera. Esse valor representa a concorrência média interna do sistema e pode ser utilizado como base para dimensionamento de consumidores, threads de processamento, partições de filas ou limites de paralelismo, servindo como fator base para antecipar degradações ou otimizações de forma proativa, sem depender de saturação. Lembrando que, com base interpretativa do modelo, quanto menor o valor de L, melhor.

Pequenos aumentos no tempo médio de processamento impactam diretamente o número de mensagens acumuladas, aumentando o risco de atraso e crescimento não controlado da fila, por exemplo, em um aumento do tempo de processamento para 85ms:

\begin{equation} L = 1.500 \times 0.085 \end{equation}

\begin{equation} L = 127 \end{equation}

Ao elevar o tempo médio de processamento, mesmo para um aumento aparentemente pequeno e plausível em cenários reais, causado por variação de payload, latência de dependências externas, I/O ou demais contenções externas, o número médio de mensagens em voo salta para 127 de concorrência interna, um aumento absoluto de 52 mensagen

Lei de Little e o “Ponto Saudável”

A Lei de Little nos fornece um critério de avaliação para encontrar um “ponto saudável” de operação de um sistema, no qual entendemos que, com o crescimento da carga (λ), não teremos aumento descontrolado da concorrência interna (L).

Para tornar isso palpável, podemos adotar um L(Alvo) para o sistema, como um Service Level de engenharia, que representa um número máximo desejável de itens em concorrência interna, sendo esse compatível com os limites físicos e operacionais da solução, nos levando à busca por otimizações constantes para reduzir o tempo de processamento (W).

Considere uma API REST que possui um L(Alvo) de 150. O sistema recebe 500 requisições por segundo, com um tempo médio de resposta de 300ms. Pela Lei de Little:

\begin{equation} L = 500 \times 0.3 \end{equation}

\begin{equation} L = 150 \end{equation}

Esse cenário caracteriza o contrato do “Ponto Saudável”, onde o sistema opera dentro do limite planejado de concorrência interna e mantém uma certa previsibilidade e margem para absorver variações. À medida que a carga cresce no sistema para 1000 requisições por segundo, o L vai para 300, ultrapassando o L(Alvo) e podendo levar o sistema para uma região de saturação e risco.

Uma progressão saudável nos leva à pesquisa interna para lidar com uma redução proporcional do tempo de processamento W. Aqui aplicamos diversas técnicas de otimização para diminuir o tempo de processamento dos requests. Podemos descobrir o tempo-alvo para otimização (W) dividindo nosso L(Alvo) pela taxa de requisições recebidas (λ) atual e multiplicando, de forma categórica, para chegar à mesma unidade de tempo que estamos utilizando — no caso do exemplo, milissegundos:

\begin{equation} W = \frac{\text{L(Alvo)}}{\lambda} \times 1000 \end{equation}

Convertendo para o exemplo da nossa API:

\begin{equation} W = \frac{150}{1000} \times 1000 \end{equation}

\begin{equation} W = 150ms \end{equation}

Nesse cenário, podemos entender que, para que nosso sistema volte a operar com o L(Alvo) de 150, precisamos diminuir nosso tempo de processamento (W) de 300ms para 150ms. Nesse novo formato otimizado, o sistema processa 50% mais requisições mantendo a mesma concorrência média interna. O objetivo é que o crescimento seja absorvido estruturalmente, sem acúmulo adicional de filas ou pressão excessiva sobre recursos.

Knee Curve (Curva do Joelho)

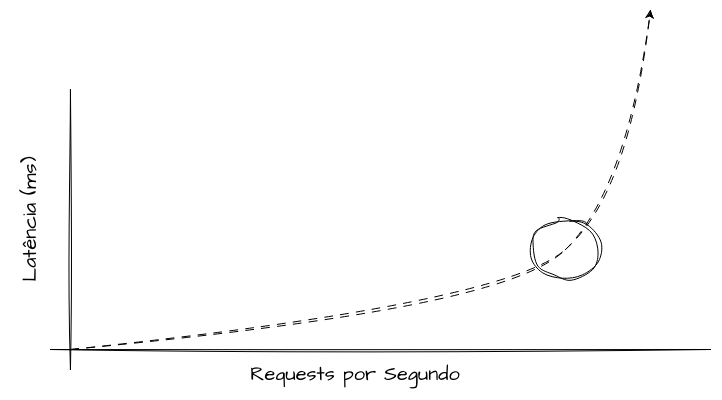
A Knee Curve, ou Curva do Joelho, é um conceito que demonstra a relação entre a utilização de um sistema e o seu ponto de degradação de capacidade. Em um teste de carga, representa o ponto onde o tempo de resposta muda drasticamente em relação à tendência anterior.

Em termos normais, a latência cresce de forma linear conforme a quantidade de requisições que um sistema está lidando aumenta. A Curva do Joelho revela o ponto a partir do qual o sistema deixa de se comportar de forma previsível e passa a apresentar degradação acelerada.

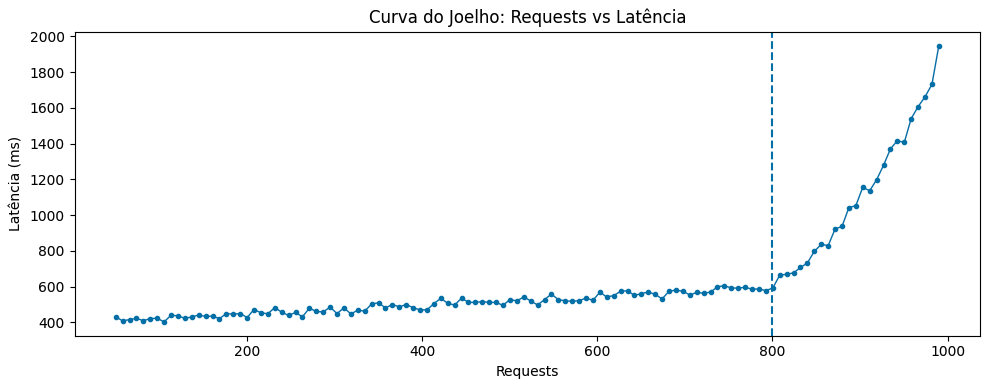
Enquanto a utilização está antes da formação do “joelho”, o sistema tem capacidade de operar de forma saudável e segura e absorver pequenas variações de carga. Operar próximo ou além da curva aumenta significativamente o enfileiramento interno de recursos, o número de retries e a saturação dos componentes.

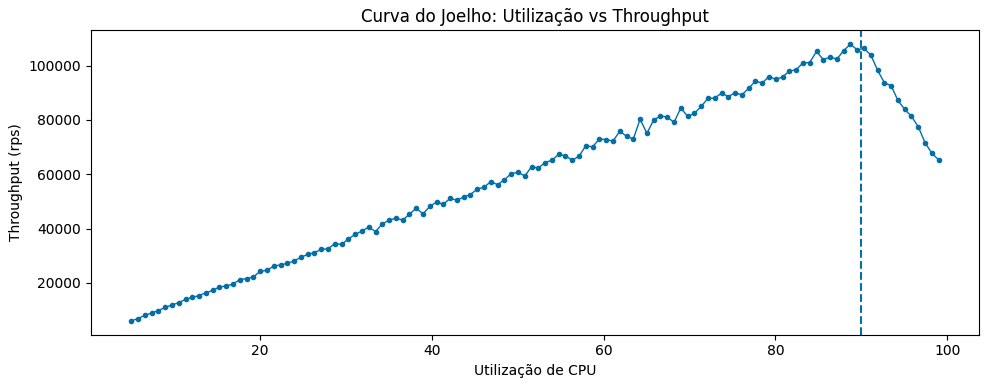
Podemos aplicar o modelo a outras métricas além de requests propriamente ditos. É possível utilizar recursos físicos como CPU e memória para entender a partir de que ponto de uso o sistema começa a degradar em throughput e latência, e, a partir disso, estimar suas capacidades e definir automações preventivas de auto scaling de forma mais assertiva.

Em paralelo à Teoria das Filas, à medida que a utilização cresce e se aproxima da capacidade máxima ou ultrapassa o “Ponto Saudável” definido pela Lei de Little, as filas internas começam a se formar e o tempo de espera passa a ser dominante em relação a todo o tempo de processamento definido. A partir desse ponto, a latência cresce de forma não linear, frequentemente exponencial, mesmo quando o aumento de utilização adicional é pequeno ou aparentemente irrelevante.

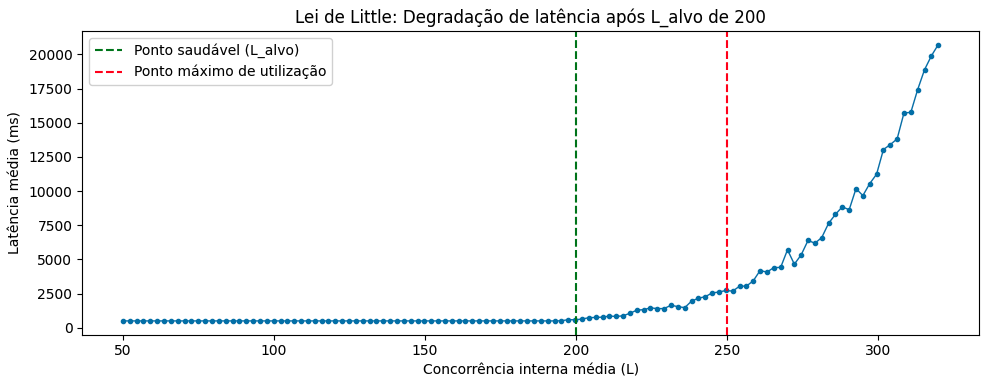
Em testes de performance, encontrar a curva do joelho do sistema permite identificar dois pontos importantes: o “Ponto Saudável” e o “Ponto Máximo de Utilização”. O Ponto Saudável, normalmente, é uma zona anterior à Curva do Joelho onde existe o maior equilíbrio operacional entre eficiência e previsibilidade. Dentro desse intervalo, entendemos que o throughput cresce de forma saudável e os tempos de resposta permanecem conhecidos e controlados.

Já o Ponto Máximo de Utilização corresponde ao limite teórico em que o sistema ainda processa requisições, porém à custa de latências elevadas, alta imprevisibilidade e risco significativo de indisponibilidade e falhas na experiência do usuário. O ideal é que ambas as zonas se estabeleçam antes da curva do joelho definitiva: uma para operação normal e outra para definição explícita do limite máximo de risco aceitável.

Margens Seguras de Saturação

Quando olhamos para recursos físicos sob a ótica de capacity planning, como, por exemplo, a utilização de CPU, não devemos interpretá-los com o objetivo de maximização como prioridade, mas sim como recursos finitos com margens de proximidade instáveis.

Quando comparamos, por exemplo, CPU e memória com outros recursos como largura de banda, armazenamento e IOPs, suas saturações não se manifestam de maneira linear e não representam recursos definitivamente livres para serem alocados como um simples “espaço disponível”. Esse fenômeno pode ser interpretado por meio da Teoria das Filas. Pequenos aumentos de utilização próximos de um “Ponto Saudável” de uso de CPU provocam crescimento de filas de forma desproporcional, sem que esses limites estejam necessariamente próximos de 100% de utilização.

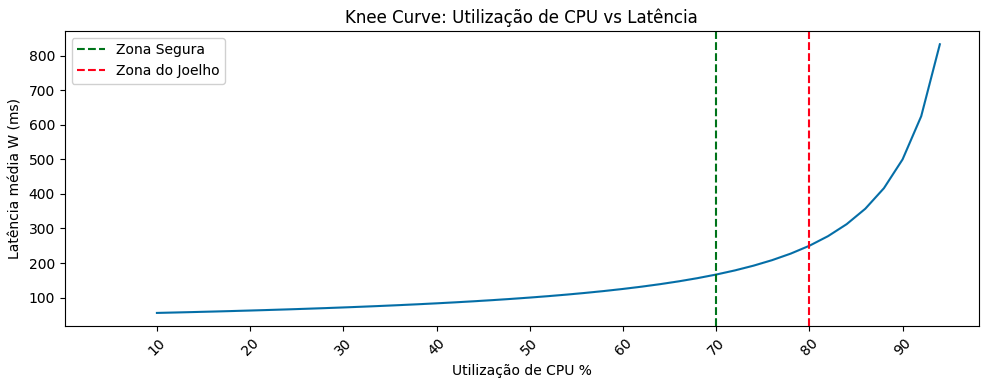
Os “Pontos Saudáveis” de CPU e memória são zonas de utilização onde o sistema consegue absorver variações de carga, como spikes, bursts e jitters, sem exaurir a taxa de processamento (μ) ou aumentar o tempo de processamento (W), evitando a geração de filas e gargalos. O ponto central é que não é necessário atingir 100% de CPU para que o sistema crie e inflacione filas internas. Próximo de 80–85% de utilização, incrementos marginais de carga já produzem aumentos desproporcionais em latência e conco

Modelagem de Carga

A modelagem de carga é um dos principais requisitos para se estimar o capacity planning de um sistema. Dentro de ambientes modernos, possuímos diversas ferramentas de monitoramento e observabilidade que coletam sinais de logs, métricas e traces emitidos pelas aplicações e seus componentes para gerar diversas dimensões de visualizações e alertas. Quando vamos estimar a capacidade de um sistema, precisamos analisar algumas delas de forma unificada e correlacionada.

Transações por segundo, requests concorrentes e o payload médio formam, em conjunto, uma representação mais fiel do comportamento real do sistema do que qualquer uma dessas métricas analisada de forma independente pode gerar. Juntas, essas três métricas formam a base mais sólida para uma modelagem de carga realista.

As Transações por Segundo descrevem o ritmo de solicitações, a concorrência descreve a pressão acumulada no sistema perante a chegada dessas solicitações, e o tamanho do payload descreve o peso individual de cada transação, a nível de networking, storage, custo de serialização e consumo de memória.

Transações por Segundo

As Transações por Segundo representam a taxa de chegada de requisições ao sistema e constituem o ponto inicial de qualquer estimativa. Nenhuma métrica é mais importante do que a quantidade de interações que um sistema recebe, ou irá receber.

Mesmo dentro do mesmo segundo, um sistema ainda pode apresentar insights valiosos sobre bursts. Dois sistemas podem operar com o mesmo TPS médio e apresentar comportamentos totalmente diferentes se a distribuição temporal dessas transações variar. Um workload com 1000 TPS distribuídos de forma homogênea ao longo do segundo impõe uma pressão completamente distinta de outro com a mesma média, porém concentrado em bursts de 5–10 ms, e conhecer esse nível de granularidade pode nos ajudar a estimar, com muito mais precisão, a capacidade necessária para suprir as demandas de forma inteligente.

Processos Concorrentes

Os requests concorrentes representam uma dimensão interna do sistema que reflete sua capacidade de processamento. Diferentemente das Transações por Segundo, que descrevem a taxa de chegada de solicitações ao sistema, os Processos Concorrentes descrevem a quantidade de trabalho simultâneo que o sistema sustenta.

Em sistemas síncronos, como servidores gRPC ou APIs REST, isso se manifesta como threads ocupadas, conexões abertas, entre outros recursos concorrentes. Em sistemas assíncronos, pode ser interpretado como mensagens em voo, partições ocupadas, consumidores ativos e taxa de processamento de eventos e mensagens em brokers.

Podemos ilustrar esse comportamento em APIs que apresentam latências aceitáveis em p95, mas mantêm concorrência interna elevada devido a pequenas degradações em dependências externas. Nesses casos, a capacidade aparente parece suficiente, enquanto o sistema já opera próximo a limites estruturais invisíveis. Ter consciência de como estimar e medir a concorrência interna é fundamental para evitar esbarrar nas “curvas do joelho” do sistema.

Tamanho de Payload

Estimar o tamanho do payload, sejam eles mensagens ou requests HTTP, é uma dimensão que é rotineiramente ignorada durante a estimativa de capacidade. Em sistemas com requisições mais homogêneas, ou seja, microserviços que possuem poucos endpoints ou contratos bem definidos de mensagens e eventos, é possível prever o tamanho desses payloads com certa precisão e estimar de forma mais confiável a pressão de tráfego de I/O que o sistema irá lidar. Porém, em sistemas que possuem múltiplas funcionalidades distribuídas em diversas filas e endpoints, o payload médio pode não representar uma dimensão fiel à realidade do sistema. O risco do erro da estimativa não está na média dessa variável, mas sim na dispersão em torno dessa média.

Payloads maiores tendem a ampliar o tempo de processamento, o consumo de memória, a pressão em garbage collection, o uso de buffers de rede e a latência de serialização. Um sistema que processa majoritariamente payloads pequenos, mas ocasionalmente recebe payloads muito maiores, pode apresentar comportamento estável na média e, ainda assim, sofrer degradações abruptas sob cenários perfeitamente válidos do ponto de vista funcional. Essa variabilidade cria caudas longas no tempo de resposta e amplifica o efeito de filas internas, mesmo sem alterações perceptíveis na TPS.

Idealmente, precisamos modelar sistemas e contratos que não sofram grande variação de tamanho. Quando isso não for possível, é necessário estimar cada uma das funcionalidades de forma isolada e se concentrar em encontrar alguma estatística que represente de maneira mais fiel o sistema diante de suas particularidades.

Cálculos de Estimativa de Carga

Podemos estimar matematicamente nossa modelagem de carga com uma série de equações simples que podem ser aplicadas a dimensões já conhecidas do sistema ou fornecidas por times de produto. A seguir, iremos abordar como expandir ainda mais a aplicação dessas equações em cenários mais específicos.

Estimativa de Transações por Segundo

Quando falamos sobre Performance, Capacidade e Escalabilidade, já ressaltamos o quanto o throughput é uma métrica extremamente valiosa e importante para entender todo tipo de comportamento do sistema. Essa métrica é a primeira a precisar ser levantada porque conecta diretamente o comportamento do usuário à pressão exercida sobre a arquitetura.

Embora simples, o TPS deve ser interpretado como um valor estatístico médio, mínimo e máximo, e não como um fluxo contínuo e uniforme. Em sistemas reais, a taxa de chegada oscila ao longo do tempo, sofre efeitos de sincronização, burstiness e correlação entre usuários ou clientes. Levantar o desvio padrão do TPS também pode fornecer insights valiosos sobre a variação do mesmo ao decorrer de certos períodos.

\begin{equation} \text{TPS} = \frac{\text{Unidades de Trabalho Processadas no Período}}{\text{Tempo em Segundos do Período}} \end{equation}

Na prática, esse valor costuma ser extraído de métricas sazonais de séries históricas, projeções de crescimento ou metas de negócio, e posteriormente ajustado para picos, sazonalidade e eventos especiais que podem acontecer em certos períodos do mês ou do ano, como promoções, ações de marketing, Black Friday, Natal, entre outros.

TPS Sistêmico

O TPS Sistêmico representa a capacidade efetiva de vazão de todo o sistema, considerando não apenas a aplicação principal, mas todas as suas dependências críticas. Em arquiteturas distribuídas, o throughput observado externamente é sempre limitado pelo menor gargalo ativo no caminho de processamento.

\begin{equation} \text{TPS Sistêmico} = \min(\text{TPS App}, \text{TPS Database}, \text{TPS Cache}, \text{TPS etc.}) \end{equation}

Não importa o quão escalável seja a camada de aplicação se o banco de dados, o cache, o broker de mensagens ou uma API externa impõem limites mais restritivos. Além disso, o gargalo dominante pode mudar dinamicamente conforme o perfil de carga, o tamanho de payload ou o tipo de operação.

Estimativa de Tamanho de Payload

A estimativa de tamanho de payload busca quantificar o volume médio de dados trafegados por requisição, considerando tanto o corpo da mensagem quanto o overhead de protocolos de transporte, como HTTP, TLS, mTLS, entre outros.

\begin{equation} \text{Payload_bytes} = (\text{Body_bytes} + \text{Headers_bytes}) \end{equation}

Entretanto, em sistemas reais, é necessário considerar camadas adicionais de overhead, como encoding, compressão, criptografia e framing de protocolo, que podem tanto ampliar quanto reduzir o tamanho efetivamente trafegado.

\begin{equation} \text{Payload_bytes} = (\text{Body_bytes} + \text{Headers_bytes}) \times \text{Overhead} \end{equation}

Mais importante do que o valor médio absoluto é a variabilidade do payload, pois payloads grandes tendem a amplificar latência, consumo de memória e tempo de processamento, criando caudas longas que afetam a estabilidade do sistema, mesmo quando a média parece controlada.

Estimativa de Bytes de Uma Transação

Enquanto o payload representa uma única mensagem, a estimativa de bytes por transação considera o custo completo de uma interação, incluindo request e response. Essa visão é mais adequada para análises de capacidade fim a fim e para estimativas de custo e banda sob carga real.

\begin{equation} \text{Payload_médio(bytes)} = \text{Request_payload} + \text{Response_payload} \end{equation}

Essa métrica se torna especialmente relevante em APIs verbosas, fluxos com respostas ricas em dados ou sistemas onde o volume de resposta cresce com o contexto da operação. Ignorar o payload de resposta é um erro comum que pode fazer muita diferença para entender divergências entre estimativas e o tráfego real.

Estimativa de Banda pelo Payload e Transações por Segundo

A estimativa de banda conecta diretamente o throughput lógico (TPS) com o consumo físico de rede. A partir do payload médio por transação, é possível estimar o volume de dados trafegados por segundo e, consequentemente, dimensionar links, limites de ingress e custos de transferência.

\begin{equation} \text{Banda_bytes/s} = \text{TPS} \times \text{Payload_médio(bytes)} \end{equation}

Esse cálculo fornece uma aproximação inicial, que deve ser refinada com fatores como retries, retransmissões, fan-out interno e replicação de tráfego entre zonas ou regiões.

Perfis de Tráfego

Os Perfis de Tráfego permitem compreender como a carga do sistema se distribui ao longo do tempo, revelando padrões de uso, assimetrias e variações que não aparecem em métricas agregadas. Ao analisar comportamentos diários, semanais e sazonais, é possível antecipar picos previsíveis, identificar janelas de ociosidade e planejar capacidade de forma proativa, alinhando desempenho, custo e previsibilidade, vamos explorar conceitualmente cada um deles.

Perfil Diário

O Perfil Diário busca estudar o comportamento de uso do sistema ao decorrer de um dia corrido, um período fechado de 24 horas. Normalmente, está associado aos hábitos e à rotina dos usuários e aos agendamentos das integrações sistêmicas. Aqui temos análises mais granulares, com agregações de poucos minutos, como 1, 2, 5 e 10 minutos, para análises de tendência. Podemos, aqui, analisar diversas estatísticas, como média, p95, p99, tempo máximo e mínimo da agregação dos requests.

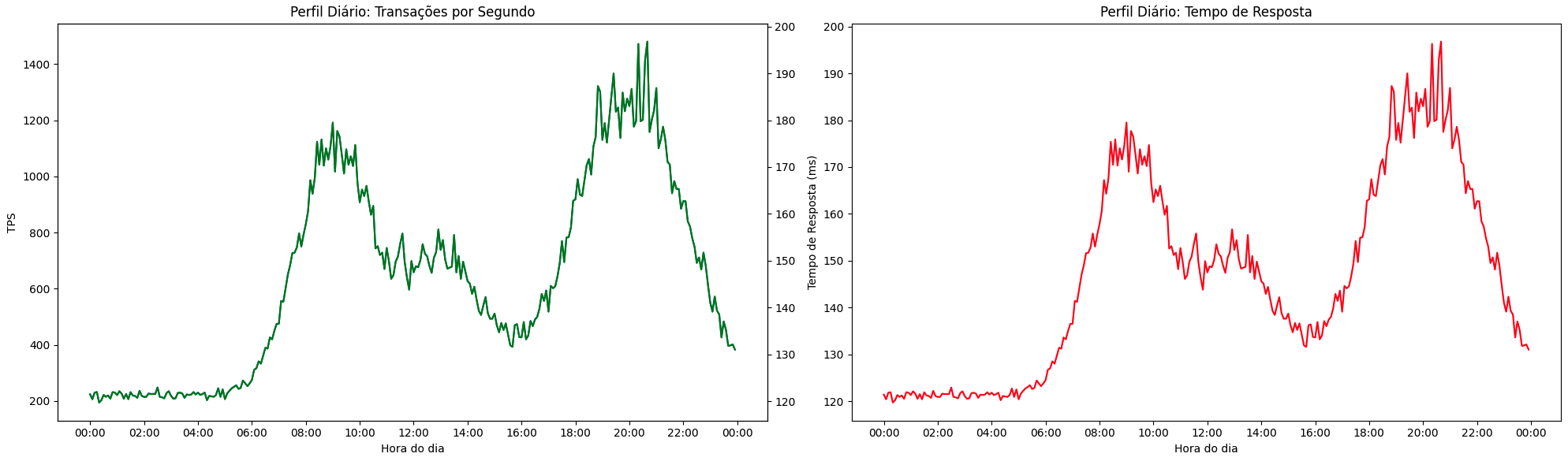
Em sistemas com finalidade operacional voltados a usuários finais, podemos entender em que momento do dia eles começam a operar dentro do sistema, normalmente tendo sua maior pressão de tráfego dentro das janelas de expediente, aliviando nos horários de almoço e ficando com pouco ou nenhum tráfego durante a noite e a madrugada. Em sistemas de delivery de comida, podemos presumir os maiores picos de uso minutos ou horas antes dos horários de almoço e jantar; em sistemas de carona, próximos do início e do fim do expediente; e, em sistemas B2B ou internos, os picos tendem a se alinhar a** rotinas operacionais, fechamentos de lote ou execuções agendadas**.

Do ponto de vista de capacity planning, o perfil diário é crítico porque define a duração dos períodos de alta e baixa utilização. Podemos utilizar esse tipo de estudo para entender os momentos do dia em que nosso tráfego irá aumentar de forma rotineira, ajustando preventivamente nossa capacidade, ou quando o sistema ficará subutilizado.

Perfil Semanal

O Perfil Semanal busca entender padrões de carga que se repetem durante os dias da semana, em um período de 7 dias, para encontrar padrões e desvios de uso, erros e latência distribuídos ao longo da semana. Para isso, utilizamos agregações de tempo maiores, como 1, 2, 3 e 5 horas, ainda aplicando estatísticas de média e percentis de forma comparativa para entender desvios e comportamentos do sistema.

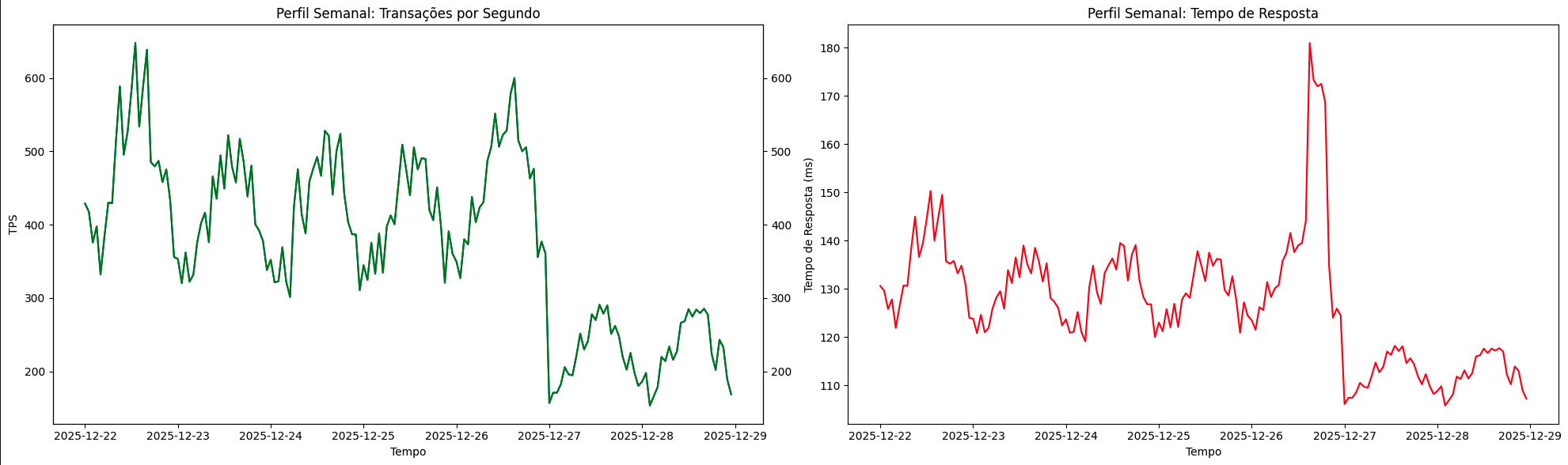
Um sistema pode operar confortavelmente abaixo do ponto saudável durante boa parte da semana e, ainda assim, entrar em regiões de saturação previsível em dias específicos. Diferente do perfil diário, que tende a ser mais suave e previsível, o perfil semanal pode introduzir assimetrias abruptas, como segundas-feiras sistematicamente mais carregadas ou sextas-feiras com picos concentrados em horários específicos, uso mais suavizado durante o restante dos dias úteis e tráfego baixo durante os finais de semana.

Esse perfil é útil para entender desvios de uso do sistema e nos ajuda a projetar capacidade com base em períodos repetitivos dentro de uma semana, nos proporcionando formas de realizar warm-ups preventivos ou descomissionamento de contêineres ou servidores em períodos de ociosidade conhecida.

Perfil Sazonal

O Perfil Sazonal descreve variações de carga em escalas mais longas, como semanas, meses ou anos, e está normalmente associado a ciclos de negócio, eventos externos ou mudanças de comportamento dos usuários. Esse tipo de dimensão nos ajuda a projetar diversas estratégias valiosas de capacity planning. Aqui, a agregação pode ser feita em períodos maiores, como dias ou semanas.

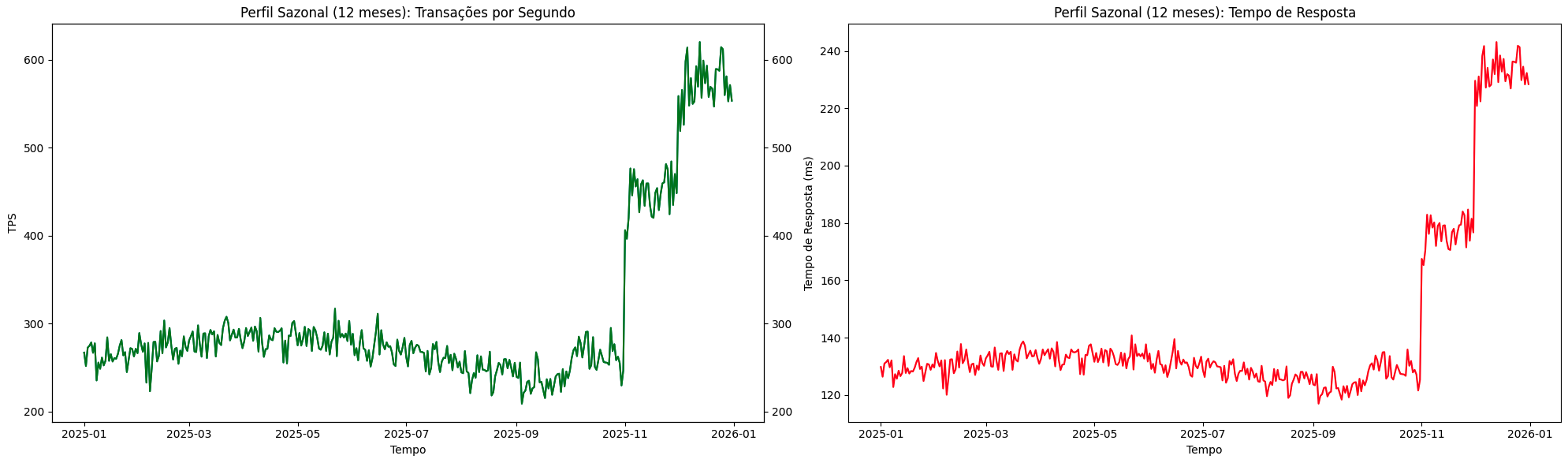
Essa estratégia nos permite estudar o crescimento gradativo do sistema e como ele se comporta em períodos específicos de fatias de tempo maiores. Exemplos comuns incluem períodos promocionais, datas comemorativas, ciclos fiscais, eventos regulatórios ou mesmo fatores externos, como clima e calendário escolar. Podemos atingir níveis de escalabilidade adequados analisando apenas períodos mensais ou semanais, mas, ainda assim, sofrer falhas de capacidade em determinados períodos não estacionários do ano que não seguem o padrão de um “mês comum” ou “semana comum”, como, por exemplo, e-commerces durante promoções de Black Friday, onde uma semana específica de novembro excede todos os padrões observados no restante do ano.

A combinação dos perfis diários para análises granulares, semanais para identificação de tendências e sazonais em nível de mês e ano nos permite elevar significativamente nossa capacidade de projetar e estimar a capacidade dos sistemas ao longo de longos períodos de forma profissional e estruturada.

Projeção de Crescimento

A projeção de crescimento é um exercício de capacity planning no qual a análise deixa de ser estática e reativa e passa a adotar estratégias de antecipação. Diferente do tópico anterior, em que as estimativas buscavam entender o sistema e compreender seus comportamentos e tendências, a projeção busca responder a uma pergunta um pouco mais difícil: como a carga do meu sistema será daqui a 3, 6 ou 12 meses?

Responder a esse tipo de pergunta exige uma análise temporal extensa do passado para entender o crescimento natural e também uma parceria com os times de negócio para compreender as expectativas e perspectivas de mercado da empresa para os produtos. A missão da engenharia é suportar as expectativas dos produtos de forma sustentável e realista, portanto, as expectativas sobre o futuro do sistema devem ser de conhecimento comum entre tecnologia e negócios.

Crescimento Linear

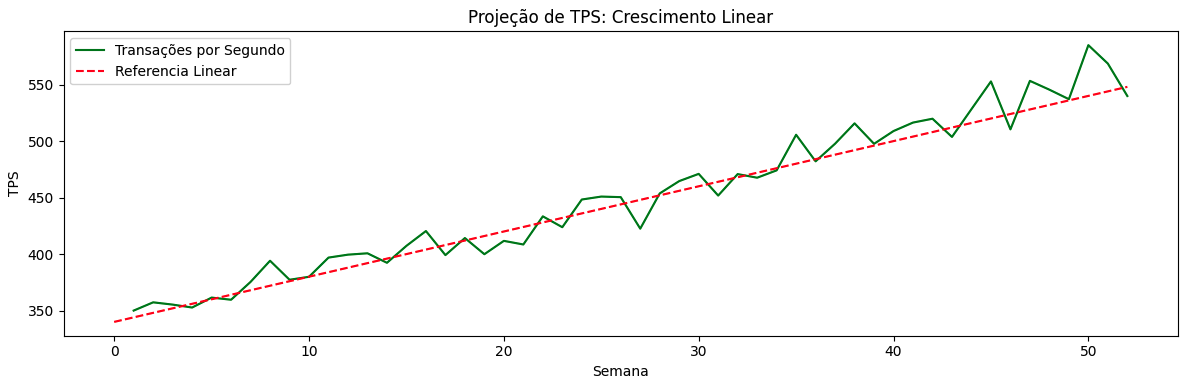
O crescimento linear assume que métricas como TPS, volume de dados ou usuários ativos aumentam de forma proporcional ao tempo. O número de usuários, licenças, transações ou compras cresce seguindo uma tendência semelhante todos os meses ou semanas. Pequenas variações dessa taxa, para mais ou para menos, não descaracterizam esse comportamento como linear nesse tipo de cenário.

Podemos encontrar esse padrão em estágios iniciais de um produto ou em sistemas muito bem estabelecidos — cenários opostos, mas que compartilham uma tendência de crescimento previsível e estável. Nesse tipo de análise, entendemos, por inferência, que dobrar a quantidade de transações ou usuários de um sistema implica diretamente em dobrar sua capacidade.

Crescimento Não Linear

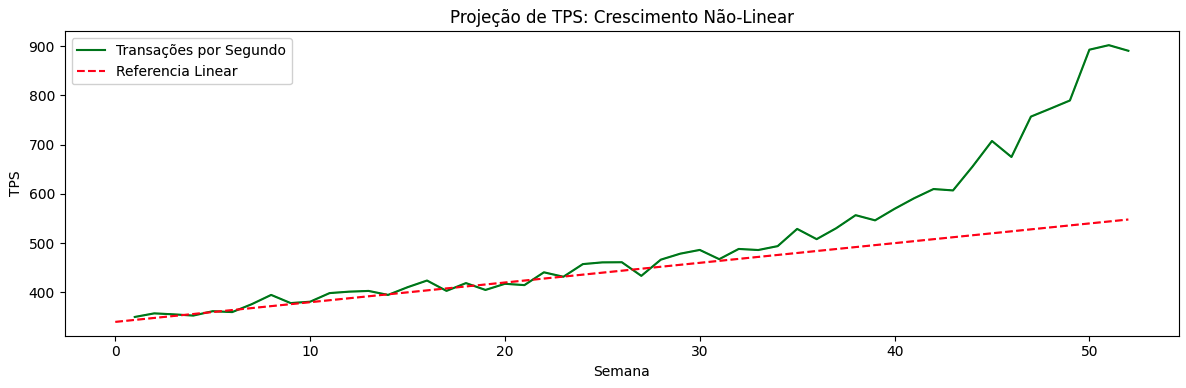
Em sistemas mais variáveis, o tráfego e a capacidade raramente crescem de forma linear, podendo apresentar comportamentos não previsíveis ao longo do tempo, alternando períodos lineares, exponenciais ou irregulares.

O crescimento não linear tende a invalidar análises de comportamento prévias. Esses cenários podem ocorrer devido a mudanças de comportamento dos usuários ou à introdução de novas funcionalidades, onde pequenas variações no número de usuários ou eventos podem gerar aumentos desproporcionais em TPS, latência ou concorrência interna. Esse tipo de variação também pode ocorrer em função de testes de estratégias de marketing e negócios, que provocam comportamentos imprevisíveis de novos usuários e cargas no sistema.

Crescimentos não lineares e não planejados podem ser extremamente perigosos para sistemas que operam próximos da sua taxa máxima de processamento conhecida.

Crescimento Mediante Novas Features e Eventos de Negócio

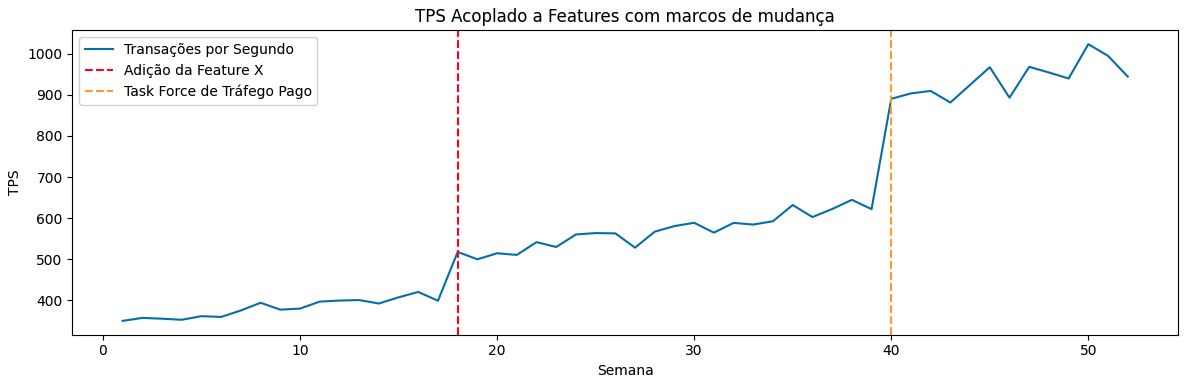
Uma dimensão extremamente significativa que nos permite atuar em conjunto com os times de negócio é a projeção de crescimento mediante mudanças, novas features e eventos planejados. O perfil de tráfego de um sistema pode se alterar de forma brusca com a introdução de novas funcionalidades, migrações de usuários ou campanhas de marketing de conversão, entre outros fatores. Ter esses eventos alinhados com os times responsáveis nos dá a oportunidade de trabalhar de forma planejada e preventiva para suportar essa nova entrada de carga.

Uma mudança ou evento de negócio voltado a atrair mais usuários para o sistema ou aumentar sua taxa de uso pode deslocar os limites de processamento, aproximando o sistema de sua “curva do joelho” de performance e capacidade com as funcionalidades já existentes. Além disso, a adição de uma nova feature pode multiplicar o número de chamadas internas por requisição, aumentar significativamente o payload médio ou introduzir dependências adicionais no fluxo sistêmico. Realizar testes de carga contemplando as características das novas funcionalidades é fundamental para reavaliar a capacidade necessária para atendê-las de forma adequada.

Nem toda mudança ou feature exige um novo planejamento de capacidade em nível de detalhe máximo, mas aquelas que têm o objetivo explícito de alterar o comportamento do sistema como um todo precisam, sim, ser consideradas para garantir maior segurança. Levantar estimativas e expectativas com todos os envolvidos nessas mudanças é essencial para planejamentos mais assertivos.

Capacidade End to End (E2E)

Avaliar a capacidade End to End de um fluxo, sistema ou transação nos ajuda a tomar responsabilidade sobre o encadeamento total entre os serviços que os compõe. Avaliar todas as dependências e integrações, como a soma de todas as capacidades individuais, revela onde o fluxo se limita, onde os gargalos emergem e quais sistemas podem falhar sobre carga real. Precisamos avaliar tanto o Throughput Individual de cada sistema para ter uma margem de avaliação e o sistêmico, onde vamos avaliar como todos os “steps” se comportam em cadeia.

Throughput individual

O throughput individual representa a capacidade máxima sustentável de um componente isolado dentro do sistema, avaliada fora do contexto completo do fluxo fim a fim. Ele descreve quanto trabalho um serviço, banco de dados, fila ou consumidor consegue processar por unidade de tempo sob condições controladas, considerando seus próprios limites de CPU, memória, I/O, concorrência e configuração interna.

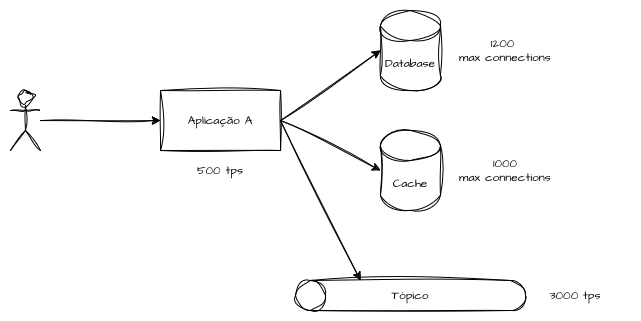
Essa dimensão pode ser avaliada em dois cenários. No primeiro, considera-se o contexto de um microserviço e suas dependências diretas, como caches, filas e bancos de dados, onde a capacidade individual é avaliada dentro de um domínio de serviço. No segundo, a análise ocorre em cada microcomponente de forma isolada. O primeiro cenário serve para avaliar uma fragmentação específica de negócio, como “quanto esse sistema de emissão de boletos consegue processar”, enquanto o segundo responde perguntas como “quanto esse banco de dados suporta de I/O” e métricas derivadas. Ambos fornecem insights valiosos sobre capacidade de produção.

Throughput sistêmico

O throughput sistêmico corresponde à capacidade máxima de um sistema ou funcionalidade, contemplando todas as suas dependências. O objetivo é ser agnóstico à capacidade individual de cada componente, levando em consideração apenas o fluxo completo, da entrada até a resposta final. Essa estratégia serve para avaliar a capacidade total da solução e identificar oportunidades de melhoria relacionadas a filas e gargalos.

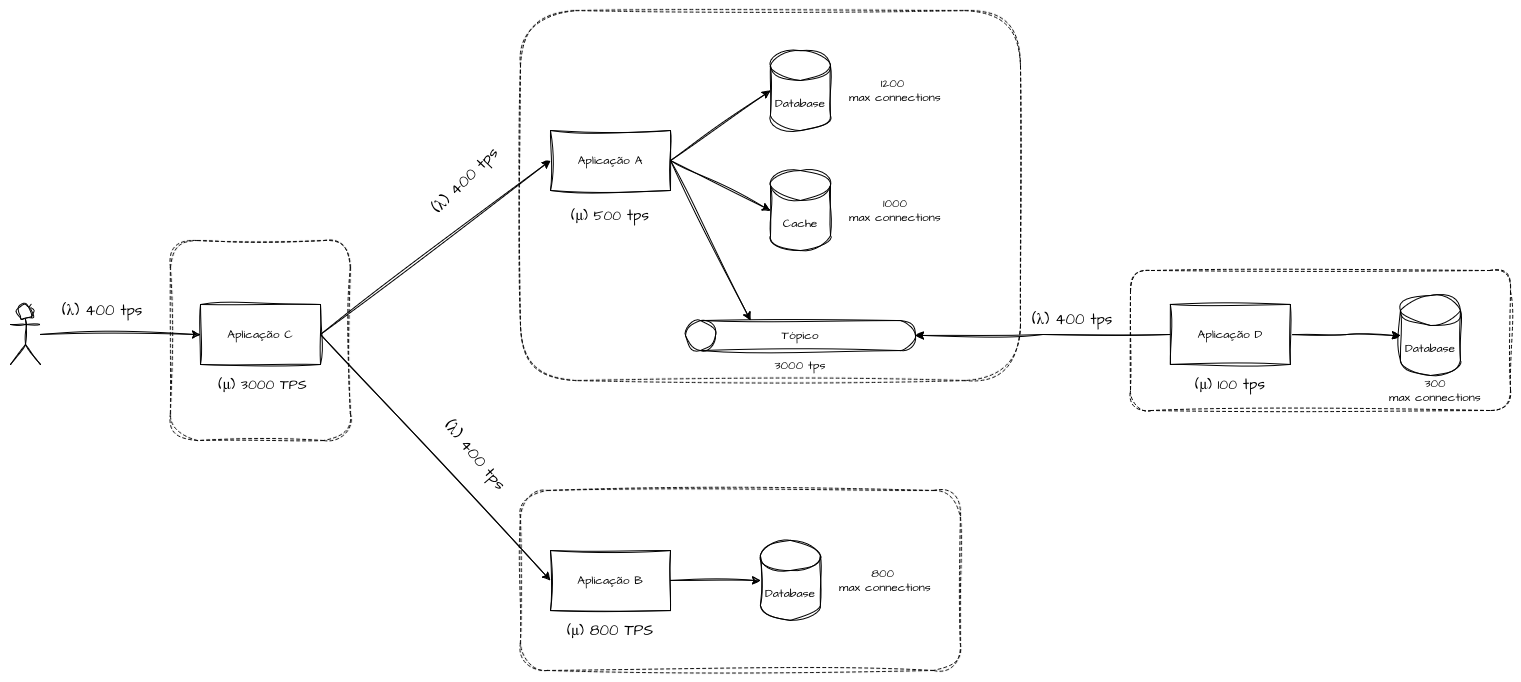
Em termos práticos, o throughput sistêmico busca identificar o ponto de desequilíbrio entre a taxa de chegada (λ) e a taxa de processamento (μ) em cada hop do fluxo, determinando qual componente exerce maior pressão contrária ao processamento fim a fim. Mesmo que serviços isolados operem com folga, o sistema como um todo pode apresentar throughput limitado quando a variabilidade de throughput e latência se acumula ao longo da comunicação end to end.

Do ponto de vista de capacity planning, medir throughput sistêmico implica observar o comportamento do sistema sob carga contínua, e não apenas picos instantâneos. Um sistema pode atingir um TPS elevado por curtos períodos e, ainda assim, não ser capaz de sustentar essa vazão ao longo do tempo, caracterizando uma capacidade apenas nominal, e não operacional.

Dependência do Gargalo

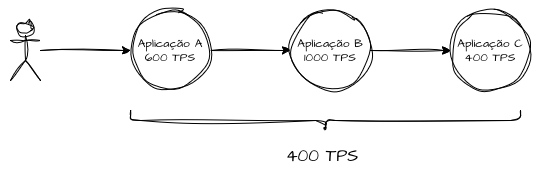
Como discutido no capítulo sobre performance, capacidade e escalabilidade, gargalos são “pontos no sistema onde o desempenho ou a capacidade são limitados devido a um componente específico que não consegue lidar eficientemente com a carga atual”. Se, para completar uma transação, é necessária a resposta de três microserviços — onde um deles consegue processar de forma saudável 400 transações por segundo, outro 600 e outro 1000 — o sistema como um todo fica limitado à menor taxa de processamento, ou seja, 400 transações por segundo. Exceder essa taxa tende a provocar filas sistêmicas e pressão crescente sobre processos, threads e dependências associadas ao ponto de gargalo, impactando todo o fluxo da aplicação.

\begin{equation} \text{Gargalo} = \min(s_1, s_2, s_3, \ldots) \end{equation}

O gargalo atual do sistema é representado pelo componente ou processo com a menor taxa de processamento (μ) em todo o fluxo. Identificar essa dependência é fundamental para direcionar melhorias de forma priorizada e estratégica. Como visto anteriormente, os gargalos também se movem com o tempo: uma otimização local pode simplesmente deslocar o gargalo para outra parte subsequente do sistema.

Planejamento de Capacidade

O objetivo desta seção é fornecer um roteiro aplicável de planejamento de capacidade, levando em conta a base teórica compilada ao longo deste capítulo. A partir daqui, apresento uma “pseudo-estrutura” de um movimento de capacity planning para que seja criado um mapa mental adaptável a diversos cenários.

Delimitar o Fluxo, Funcionalidades e Componentes

O primeiro passo a ser seguido é definir qual fluxo sistêmico está sendo avaliado. Testar “o sistema” como um todo pode levar a modelagens genéricas que não refletem com precisão a realidade esperada. Portanto, identifique as funcionalidades, os contratos, os métodos de entrada, os serviços envolvidos, os dados manipulados, as respostas geradas e para onde elas são enviadas.

Nessa fase de levantamento, precisamos listar todos os microserviços, seus bancos de dados, filas e tópicos, bem como identificar quais fluxos são síncronos, quais são assíncronos e como todos eles se comunicam entre si. Esse passo estabelece o escopo do throughput sistêmico, evitando análises locais desconectadas da experiência real do usuário.

Levantar as Estimativas de Carga

Com o fluxo definido, o próximo passo é construir a carga base, utilizando exatamente as métricas discutidas anteriormente, como o TPS médio, os picos, os perfis diários e semanais, além das datas ou períodos sazonais que indicam mudanças de comportamento e o quanto essas variações podem ocorrer.

Devemos estimar os payloads, seus tamanhos e o volume de banda que irão trafegar durante os perfis levantados. Aqui também surge a oportunidade, caso ainda não esteja claro, de alinhar com os times de produto e de negócio quais são as variáveis esperadas de tempo de resposta e disponibilidade. Tornar esses indicadores explícitos é um grande facilitador para avaliar se o capacity planning está efetivamente adequado, ou se estamos subprovisionando ou exagerando em recursos ociosos.

Neste ponto, o objetivo não é precisão absoluta, mas ordem de grandeza. O modelo inicial serve para responder à pergunta: “em que condições meu sistema opera hoje?”, evitando projeções desconexas ou irreais.

Identificação do Throughput Individual dos Componentes e Serviços

Antes de projetar crescimento, é necessário entender os limites individuais de cada componente relevante do fluxo, identificando quais deles podem exercer pressão contrária, agravar gargalos ou gerar “curvas do joelho” de forma prematura, e, principalmente, em que condições isso acontece.

Aqui lidamos com variáveis como o TPS máximo sustentável do serviço, os limites de concorrência — threads, conexões e consumers disponíveis — e a capacidade efetiva de cada uma de suas dependências, como bancos de dados, caches, brokers e APIs externas. Dependências externas podem ser mockadas em ambientes controlados para que não comprometam testes de limite operacional do serviço.

Derivação do Throughput Sistêmico

A partir dos throughputs individuais, deriva-se o throughput sistêmico, aplicando explicitamente a lógica do menor gargalo. Aqui respondemos perguntas como: qual componente limita a vazão hoje? O gargalo é rígido ou pode lidar com escalabilidade horizontal dentro de uma determinada janela de tempo? O throughput, o tempo de resposta e a taxa de erros variam de acordo com o tempo e com as oscilações de tráfego dentro dos perfis de carga identificados?

Essa etapa é uma das mais importantes do processo, pois a capacidade real emerge do encadeamento entre os serviços, e não da análise isolada de componentes.

Levantamento da Projeção de Crescimento

Com a capacidade atual compreendida, o planejamento passa a incorporar projeções, evitando o erro clássico de assumir um único crescimento linear. Nesse momento, é fundamental incluir os times de negócio e, quando necessário, níveis executivos, para entender as expectativas futuras do sistema.

O objetivo aqui não é prever o futuro com precisão, mas entender até que ponto o sistema atual consegue suportar os objetivos da empresa e identificar oportunidades de melhoria para o horizonte planejado, evitando que a evolução ocorra de forma reativa, já com a experiência do cliente degradada.

Avaliar o Custo e as Margens Operacionais

Neste ponto, o planejamento incorpora explicitamente custo e risco. A pergunta deixa de ser “quanto o sistema aguenta” e passa a ser “quanto ele aguenta com previsibilidade e custo aceitável para o negócio”. Trabalhamos com dimensões como o impacto de overprovisioning versus underprovisioning, quais regiões do “Ponto Saudável” são aceitáveis do ponto de vista orçamentário e como isso se relaciona com a zona de pré-joelho de throughput e latência do sistema.

Aqui, a capacidade passa a ser tratada como orçamento, e não apenas como um limite técnico.

Definição dos Limites Operacionais

O resultado do capacity planning não deve ser um único número de “quanto aguenta”, mas sim um conjunto de limites operacionais bem definidos, como o TPS sustentável, o L(Alvo), a latência máxima aceitável (em termos de média e percentis) e a taxa de erro máxima tolerável. Essas definições precisam ser amplamente conhecidas entre os stakeholders do produto, pois também ajudam a identificar pontos futuros onde uma reavaliação arquitetural será necessária, alinhando expectativas de orçamento e planejamento estratégico.

Testes de Carga e Estresse

O último passo é validar, na prática, se o sistema atende aos requisitos estabelecidos e se possui as parametrizações adequadas para escalar de forma dinâmica ou estática. Aqui, devemos executar testes de carga média (Average Load), estresse, spikes conhecidos e testes de breakpoint para identificar quando o sistema ultrapassa o L(Alvo) e onde ele efetivamente entra em colapso.

Esses testes podem ser realizados de forma pontual, mas o ideal é que sejam executados por períodos prolongados, aproximando-se de cenários reais de operação. É fundamental coletar evidências e documentar a capacidade real, e, quando gargalos ou oportunidades de melhoria forem identificados, direcioná-los ao backlog para tratamento e priorização.

Referências

Improving the performance of complex software is difficult, but understanding some fundamental principles can make it easier.

Teoria das Filas

Elementos das Teorias das Filas

Lei de Little (Little’s Law): A Ciência por Trás de Fazer Menos e Entregar Mais

Little’s law

Knee of a curve

The “Knee” in Performance Testing: Where Throughput Meets the Wall

A Capacity Planning Process for Performance Assurance of Component-Based Distributed Systems

Capacity Planner - Google